In section one, I introduced M (Manfred) and ū (ūlina), who are N’s (Norbert’s) parents, and Norbert and ānna are Paprika’s parents.. but if you ask P personally: “Hey P, who are your parents?” He will say, well of course N is my dad.. but he wouldn’t mention his mom, because his family tree looks like:
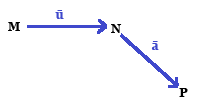
In this world, Males are the only family members (points), with females being the links between the males (vectors).
But one would ask, didn’t we just say that M
ū can equal one and only one N… Yes. But aren’t there many points that can lie on a vector, perhaps lying on ū? i.e. a point Andy can be an element of ū?… yes
But isn’t this a contradiction? No.
Because … a woman COULD have many children in her “life” (or length of this vector – that assumes she dies after having her child… sad), aka she could have an infinite amount of eggs (according to newest research); thus Andy (A) is element of ū looks like: 
.
If Manfred and ū had mated earlier, then A would have been born instead of N, but as a consequence, the life of ūlina would have been shorter (visually, the vector ū would have been shorter by a factor of lambda λ. Let’s write this hypothetical situation mathematically:
Mλū = A.
so if lambda = 0.5, A would have been born only if M and ū mated at half the life-time of ū.
To come full circle, Now imagine the E, Ē and ExĒ (Affine space with afore mentioned properties) are permeable. Like layers in Adobe Photoshop, we can place one on top of the other. If the layers are not completely opaque, the layer below will show through.
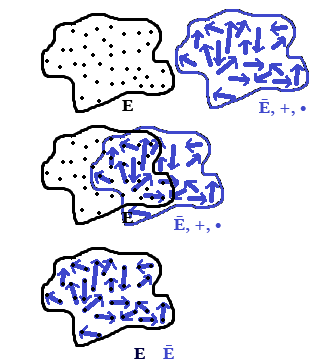
The purpose of this is to point out that every time a point like M and a vector like ū mate and create N, N is in fact also in E. It’s like shining a light through E -> Ē -> ExĒ.